14 martie nu este nici o zi obișnuită a Pi. Pasionații de matematici de pretutindeni sărbătoresc evenimentul ca Ultimate Pi Day, deoarece data va corespunde primelor cinci cifre ale pi (3.1415) și nu doar primelor trei cifre. Această confluență matematică nu se va mai întoarce timp de un secol, pe 14 martie 2115.
Continut Asemanator
- Lumea este plină de cercuri
Definit ca raportul circumferinței unui cerc la diametrul său, pi ( π ) este atât un număr transcendental cât și un număr irațional, ceea ce înseamnă că nu poate fi niciodată scris ca raportul a două numere întregi și continuă la nesfârșit fără niciun tipar repetabil. Pi nu este singurul număr irațional - există și numărul lui Euler (e) și raportul de aur ( φ, sau phi), de exemplu. Dar continuă să fie o sursă de fascinație, deoarece originile sale sunt ușor de explicat, spune Mario Livio, astrofizician la Institutul de Știință a Telescopului Spațial din Maryland.
„Toată lumea poate înțelege cum derivă pi. Toate celelalte numere sunt mai complexe. Numărul phi, de exemplu, implică o diviziune particulară a unei linii, iar numărul e necesită să știți ce este un logaritm ”, spune Livio, autorul cărții Is God a Mathematician?
O altă mare parte a apelului lui pi este că are un aspect neobișnuit pentru apariția în formule matematice, multe dintre ele fiind importante pentru procesele de zi cu zi, de la procesarea imaginilor la navigarea prin GPS. Iată doar o mică eșantionare a formulelor utilizate frecvent care includ pi:
Transformarea Fourier
Numit pentru matematicianul francez Jean-Baptiste Joseph Fourier, acest instrument matematic descompune un semnal în frecvențele sale componente - mai degrabă ca modul în care o coardă muzicală poate fi defalcată în notele sale componente. În esență, transformările Fourier sunt ideale pentru procesarea semnalelor bazate pe unde, cum ar fi sunet sau lumină și modele de găsire. Acest lucru face ca Fourier să se transforme într-un instrument fundamental în lumea digitală modernă.
„A fost numit cel mai important algoritm dezvoltat vreodată de omenire. Acum este posibil să fie hiperbole, dar poate nu este ”, spune Glen Whitney, fondatorul și directorul Muzeului Național de Matematică din New York. Transformările Fourier sunt folosite tot timpul pentru curățarea imaginilor digitale, pentru auto-Tune stele pop și pentru a găsi planete îndepărtate care orbitează alte stele. Instrumentul este, de asemenea, crucial pentru funcțiile de voce la text, care sunt acum standard pentru smartphone-uri. „Când folosiți Siri sau Google Now, unul dintre primii pași este să vă luați vocea și să efectuați o transformare Fourier pe ea ... se dovedește a fi mult mai ușor să recunoașteți vocalele când priviți transformările lor Fourier decât atunci când priviți Semnalele originale în sine ”, spune Whitney.
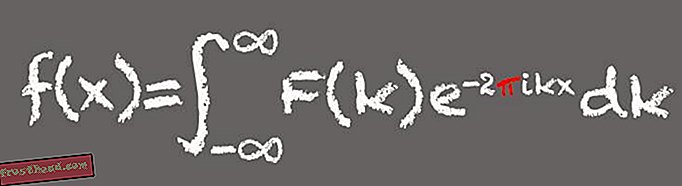(Ilustrație de Victoria Jaggard) Pi apare în transformarea Fourier deoarece una dintre părțile componente sau expresiile formulei este asociată cu sinusul și cosinusul și unghiurile create de o particulă care se deplasează în jurul unui cerc. „Ori de câte ori aveți o formulă care se ocupă de cercuri sau unghiuri, nu veți fi surprinși atunci când pi apare”, spune Whitney.
Principiul incertitudinii Heisenberg
Unul din pilonii mecanicii cuantice, principiul incertitudinii lui Heisenberg afirmă că un observator nu poate cunoaște atât poziția, cât și viteza unei particule subatomice simultan. În schimb, cu cât este cunoscută mai exact poziția unei particule, cu atât mai puțin poate fi cunoscută despre viteza ei.
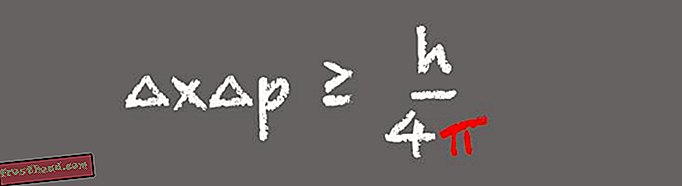(Ilustrație de Victoria Jaggard) Apariția pi în principiul incertitudinii lui Heisenberg are sens atunci când vă dați seama că în formulă, poziție și moment sunt transformări Fourier una de cealaltă, spune Whitney. Principiul incertitudinii este important în lumea modernă, deoarece descrie comportamentul particulelor de lumină, sau fotoni, în sistemele de comunicații cu fibră optică. „Ce ne spune este că nu putem cunoaște atât poziția, cât și impulsul fotonilor cu o precizie extremă. Nu puteți proiecta protocoale de comunicații care încalcă principiul incertitudinii lui Heisenberg, deoarece acestea nu vor funcționa. ”
Legea lui Stoke
Legea lui Stoke calculează forța necesară pentru a muta o mică sferă - adică un cerc tridimensional - printr-un fluid vâscos la o anumită viteză. Are aplicații în domenii, de la științele Pământului la medicină.
(Ilustrație de Victoria Jaggard) „Legea se referă în special la efectul vâscozității asupra unei sfere din fluid”, spune Whitney, care este modul în care pi intră în joc. În ceea ce privește utilizările practice ale legii lui Stoke, nu căutați mai departe de mașina dvs. „Timp de zeci de ani, modul în care companiile s-au asigurat că uleiul tău motor avea vâscozitatea potrivită pentru mașina ta era să arunce literalmente o serie de sfere de testare în ulei și să măsoare timpul necesar pentru ca acestea să treacă prin lichid”, spune Whitney. Astăzi, cel mai obișnuit mod de a măsura vâscozitatea uleiului implică un instrument numit un viscometer cu tub capilar, fără a fi necesare sfere - dar totuși raportează rezultatul în unități de măsură numite centistokes.
Formula lui Euler
Numită după matematicianul elvețian Leonard Euler, versiunea acestei formule care include pi adună unele dintre cele mai interesante numere din matematică într-un singur loc:
(Ilustrație de Victoria Jaggard) „Toată lumea crede că acest lucru este incredibil. Toate aceste numere pe care le considerăm speciale apar într-o ecuație frumoasă ”, spune Livio. În timp ce această formulă pithy poate inspira uimire în matematicieni, forma mai utilă a ecuației este puțin mai lungă:
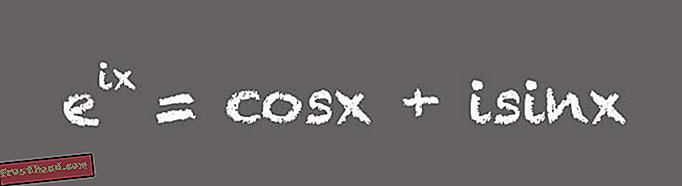(Ilustrație de Victoria Jaggard) Această versiune neambalată a formulei Euler este un instrument incredibil, spune Whitney. De exemplu, este important pentru proiectarea electronicelor care utilizează curent alternativ sau curent alternativ. „Formula lui Euler în formă extinsă înseamnă că puteți utiliza numere complexe sau imaginare, pentru a analiza și proiecta circuite AC”, spune Whitney. Asta pentru că într-un circuit de curent alternativ, tensiunea este o cantitate care oscilează în timp - de obicei de 60 de ori pe secundă, de exemplu, în alimentarea electrică standard din SUA. „Versiunea completă a formulei lui Euler ne învață cum putem folosi numere complexe ca o prescurtare convenabilă pentru modelarea fenomenelor oscilante”, spune Whitney.
Ecuațiile de câmp ale lui Einstein
O componentă de bază a teoriei sale generale despre relativitate, ecuațiile de câmp ale lui Albert Einstein descriu modul în care gravitația din masă și energie creează curbura spațiului-timp.
(Ilustrație de Victoria Jaggard) „Descrierea acestei curburi implică geometrie și, din moment ce definiția inițială a pi provine de la geometrie, aspectul în această ecuație nu este atât de surprinzător”, spune Livio. Pe lângă dezvăluirea unui adevăr fundamental despre modul în care funcționează universul, relativitatea generală are multe aplicații practice. De exemplu, sateliții care alcătuiesc Sistemul global de poziționare folosit pentru navigație ar fi fără nicio sincronizare unul cu altul, dacă inginerii nu ar ține cont de efectele de dilatare a timpului prevăzute de teorie.
